CÁC BÀI TOÁN LỚP 5 NÂNG CAO LỚP 5, CÁC DẠNG TOÁN LỚP 5 CƠ BẢN, NÂNG CAO

Con sinh vào năm 2009	https://zalo.me/g/cieyke829
Con sinh năm2010	https://zalo.me/g/seyfiw173
Con sinh vào năm 2011	https://zalo.me/g/jldjoj592
Con sinh năm2012	https://zalo.me/g/ormbwj717
Con sinh năm 2013	https://zalo.me/g/lxfwgf190
Con sinh năm 2014	https://zalo.me/g/bmlfsd967
Con sinh năm 2015	https://zalo.me/g/klszcb046

Trong chương trình toán 5, các dạng bài xích tập về tính chất nhanh luôn luôn là những dạng bài bác tập hay với khó. Các con không chỉ việc nắm được quy tắc giám sát cơ phiên bản mà còn cần phải có những khả năng quan sát, áp dụng linh hoạt các đặc thù của bốn phép toán. Để giúp những con đoạt được những việc khó này, thầy Nguyễn Thành Long – trong những giáo viên số 1 của khối hệ thống giáo dục Vinastudy chúng tôi xin gửi đến quí PHHS và các con học sinh thân yêu bài giảng “Tư duy bài toán tính cấp tốc phân số” này. ý muốn rằng đoạn clip sẽ giúp các con gồm thêm những kiến thức và kỹ năng bổ ích.

Bạn đang xem: Các bài toán lớp 5 nâng cao

kiến thức cần nhớ. cộng trừ những phân số cùng chủng loại số:

Quy tắc: mong muốn cộng (hoặc trừ) nhị phân số cùng mẫu số, ta cùng (hoặc trừ) nhị tử số cùng nhau và không thay đổi mẫu số.

Ví dụ. $frac56+frac86=frac136$

Lưu ý. sau thời điểm làm phép tính cùng (hoặc trừ) nhì phân số, nếu chưa thu được phân số về tối giản thì ta cần rút gọn thành phân số tối giản.

cộng trừ những phân số khác chủng loại số:

Quy tắc: hy vọng cộng (hoặc trừ) hai phân số khác chủng loại số, ta đề nghị quy đồng nhị phân số kia rồi cùng (hoặc trừ) nhì phân số vẫn quy đồng. 

Ví dụ. $frac16+frac25=frac530+frac1230=frac1730$

tính chất của phép cùng phân số.

- đặc điểm giao hoán. Khi thay đổi chỗ các phân số trong một tổng thì tổng của bọn chúng không nạm đổi.

Ví dụ. $frac56+frac86=frac86+frac56$

- Tính chất kết hợp. Khi cùng một tổng hai phân số với phân số thứ bố thì ta có thể cộng phân số thứ nhất với tổng nhì phân số còn lại.

Ví dụ. $frac56+left( frac16+frac116 ight)=left( frac56+frac16 ight)+frac116=1+frac116=frac176$

- Cộng với 0. Phân số nào cộng với 0 cũng chính bởi phân số đó.

Ví dụ. $frac56+0=frac56$

Lưu ý. Ta thường áp dụng các tính chất của phép cùng phân số trong số bài tính nhanh.

Phép nhân phân số.

Quy tắc: mong mỏi nhân nhì phân số, ta đem tử số nhân cùng với tử số, mẫu số nhân với chủng loại số. Vào trường hợp bao gồm thừa số là số trường đoản cú nhiên, ta nhân số tự nhiên đó cùng với tử số của phân số và giữ nguyên mẫu số.

Chú ý. Trước lúc tính, hoàn toàn có thể rút gọn gàng phân số (nếu cần)

Ví dụ $frac56 imes 7=frac5 imes 76=frac356$

đặc điểm của phép nhân phân số.

- đặc điểm giao hoán. Khi đổi chỗ những phân số trong một tích thì tích của chúng không thế đổi.

Ví dụ. $frac56 imes frac86=frac86 imes frac56$

- đặc thù kết hợp. Lúc nhân một tích nhị phân số cùng với phân số thứ ba thì ta hoàn toàn có thể nhân phân số trước tiên với tích nhì phân số còn lại.

Ví dụ. $frac56 imes left( frac610 imes frac116 ight)=left( frac56 imes frac610 ight) imes frac116=frac12 imes frac116=frac1112$

- Nhân cùng với 0. Phân số nào cộng với 0 cũng chính bằng 0.

Ví dụ. $frac56 imes 0=0$

Lưu ý. Ta thường áp dụng các đặc điểm của phép cùng phân số trong số bài tính nhanh.

đối chiếu hai phân số.

- đối chiếu hai phân số cùng chủng loại số:

Phân số nào gồm tử số nhỏ thêm hơn thì nhỏ bé hơn
Phân số nào tất cả tử số lớn hơn vậy thì lớn hơn.Nếu tử số đều nhau thì nhì phân số đó bằng nhau.

- đối chiếu hai phân số khác mẫu mã số: ta rất có thể quy đồng mẫu mã số hai phân số đó rồi so sánh những tử số của chúng.

Ví dụ

Ví dụ 1. Tính nhanh.

$ extA=frac11 imes 2+frac12 imes 3+...+frac199 imes 100$

Phân tích.

Tử số đều bằng 1.Hiệu nhì thừa số sống dưới mẫu = 1 = Tử số

Ta có: $frac11 imes 2=frac2-11 imes 2=frac21 imes 2-frac11 imes 2=frac11-frac12$

$frac12 imes 3=frac3-22 imes 3=frac32 imes 3-frac22 imes 3=frac12-frac13$

$frac199 imes 100=frac100-9999 imes 100=frac10099 imes 100-frac9999 imes 100=frac199-frac1100$

Vậy: < extA=1-frac12+frac12-frac13+...+frac199-frac1100>

$ extA=1-frac1100=frac99100$

Chú ý: Hiệu hai thừa số dưới mẫu bởi tử số: $fracb-aa imes b=frac1a-frac1b$

Ví dụ 2. Tính nhanh.

$ extB=frac11 imes 4+frac14 imes 7+frac17 imes 10+...+frac197 imes 100$

Phân tích.

Tử số đều bởi 1.Mẫu số = tích hai thừa số

Hiệu nhị thừa số ở dưới mẫu = 3

$ o $ Vấn đề. Tử số khác hiệu 2 vượt số bên dưới mẫu

$ o $ Giải pháp. Tử số bằng hiệu 2 quá số bên dưới mẫu

$ o $ Làm cố nào?

$3 imes extB=3left( frac11 imes 4+frac14 imes 7+frac17 imes 10+...+frac197 imes 100 ight)$

$ extB=frac31 imes 4+frac34 imes 7+frac37 imes 10+...+frac397 imes 100$

Vậy: < extB=1-frac14+frac14-frac17+...+frac197-frac1100>

$3 imes extB=1-frac1100=frac99100$ cần $ extB=frac33100$

Dạng toán mở rộng:

Ví dụ 1. Tính tổng: $ extC=frac12+frac14+frac18+frac116+frac132+frac164+frac1128$

Phân tích.

Tử số đều bởi 1.Mẫu số của phân số đứng sau gấp 2 lần mẫu số phân số đứng trước

Ta có: $frac14=frac2-14=frac24-frac14=frac12-frac14$;

$frac18=frac2-18=frac28-frac18=frac14-frac18$

Tương từ như thế:

$frac116=frac18-frac116$

$frac132=frac116-frac132$

$frac164=frac132-frac164$

$frac1128=frac164-frac1128$

Vậy $ extC=frac12+frac12-frac14+frac14-frac18+frac18-frac116+frac116-frac132+frac132-frac164+frac164-frac1128$

Một số bài xích tập.

Ví dụ 1. Một miếng bìa hình bình hành tất cả chu vi là 2m. Nếu bớt cạnh đi 20cm thì ta được miếng bìa hình thoi có diện tích 6dm2. Tìm diện tích miếng bìa hình bình hành đó.

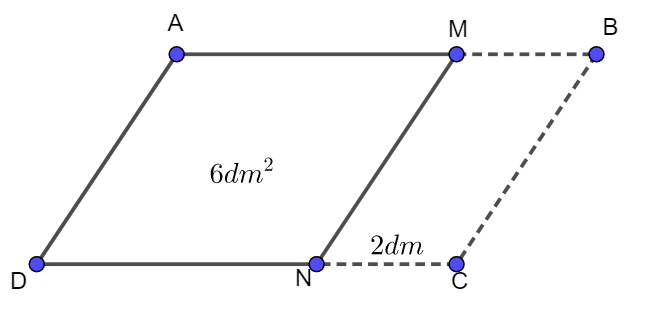
Phân tích tìm phía giải:

Trước hết phải thấy rằng các form size đã nêu trong bài xích chưa cùng đơn vị đo. Cần đổi về đơn vị đề-xi-mét để dễ dàng hơn khi tính toán.

Chu vi của hình thoi AMND tính được vì chưng đã biết chu vi hình bình hành ABCD và các đoạn MB, NC.

Hình thoi gồm 4 cạnh bằng nhau. Biết chu vi công thêm được số đo cạnh.

Tính được độ cao của hình thoi AMND. Đây cũng đó là chiều cao hạ từ A của hình bình hành ABCD. Từ đó tính được diện tích.

Lời giải:

Đổi 2m = 20dm; 20cm = 2dm

Cạnh của hình thoi là:

(20 – 2 – 2 ) : 4 = 4 (dm)

Chiều cao hạ từ A xuống CD là:

6 : 4 = 1,5 (dm)

Cạnh AB là: 4 + 2 = 6 (dm)

Diện tích hình bình hành ABCD là:

1 ,5 x 6 = 9 (dm2)

Ví dụ 2. mang lại hình thang ABCD gồm đáy bé dại AB nhiều năm 10cm có diện tích s 210cm2. Kéo dãn dài đáy lớn CD về phía C một đoạn CE = 8cm thì diện tích tăng thêm 60cm2. Tính độ nhiều năm đấy to CD.

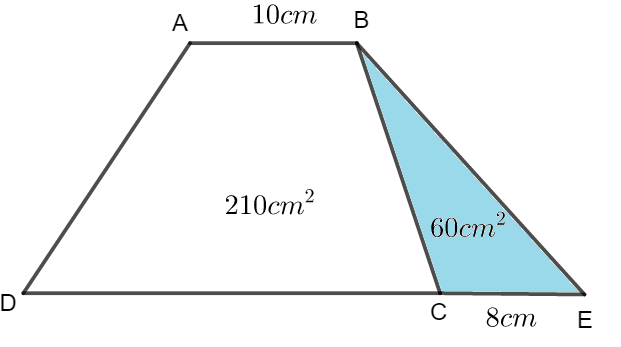
Phân tích tìm phía giải:

Nhận thấy độ cao của hình thang ABCD cũng bằng độ cao hạ từ bỏ B xuống cạnh CE của tam giác BCE. Tính được độ cao này kế tiếp áp dụng công thức để tìm kiếm độ dài đáy lớn.

Lời giải:

Chiều cao hạ từ B của tam giác BCE (cũng là độ cao của hình thang ABCD) là: 2 x 60 : 8 = 15 (cm)

Tổng hai đáy của hình thang ABCD là:

210 x 2 : 15 = 28 (cm)

Độ nhiều năm đáy bự CD là:

28 -10 = 18 (cm)

Đáp số: 18cm

Ví dụ 3. Cô trâm trồng hoa bên trên một thửa ruộng hình thang vuông bao gồm đáy lớn bởi 160m và chiều cao bằng 30m. Nếu mở rộng thửa ruộng thành mảnh đất nền hình chữ nhật cơ mà vẫn giữ nguyên đáy mập thì diện tích s thửa ruộng tăng lên 600m2. Hỏi cô Trâm bán tốt bao nhiêu chi phí hoa trên thửa ruộng đó biết rằng trung bình mỗi hec-ta hoa bán tốt 140 000 000 đồng.

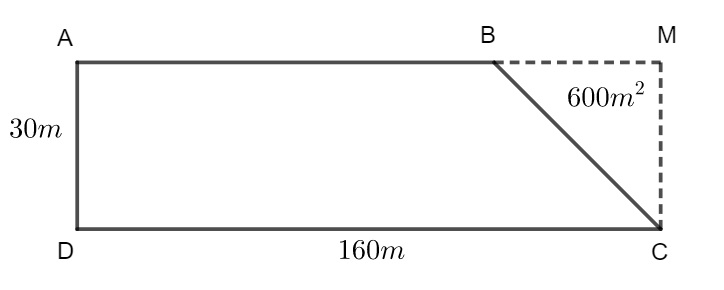
Phân tích tìm hướng giải.

Để tính được số tiền bán hoa của cô ấy Trâm ta phải tìm kiếm được diện tích của thửa ruộng hình thang ABCD. Mong mỏi tính được diện tích s hình này, ta nên tìm ra độ lâu năm đáy bé nhỏ AB. Độ nhiều năm AB thì tính được bằng cách lấy AM trừ BM, AM đó là chiều dài của hình chữ nhật AMCD còn BM lại nên đi tìm.

Xem thêm: Các loại kem đánh răng nuốt được mẹ nên biết, top 5 kem đánh răng nuốt được cho bé mẹ nên biêt

Vì ABCD là hình thang vuông nên AD đó là chiều cao và cũng bởi với chiều cao kẻ từ bỏ C của tam giác MCB. Từ kia tính BM.

Lời giải:

Độ nhiều năm đoạn BM là:

600 x 2 : 30 = 40 (m)

Đáy nhỏ nhắn AB dài là: 160 – 40 = 120 (m)

Diện tích của hình thang là:

(120 + 160) x 30 : 2 = 4200 (m2)

Đổi 4200m2 = 0,42ha.

Số tiền cô trâm thu được bên trên thửa ruộng kia là:

0,42 x 140000000 = 58800000 (đồng)

Đáp số: 58 800 000 đồng.

Ví dụ 4. Một hình chữ nhật có chu vi 54cm. Ví như tăng chiều rộng lớn thêm 2,5cm và bớt chiều dài 2,5cm thì được một hình vuông. Tính diện tích s hình chữ nhật đó.

Phân tích tìm phía giải.

Bài toán cho biết chu vi hình chữ nhật, tự đó có thể tính được tổng chiều dài với chiều rộng.

Khi tăng chiều rộng thêm 2,5cm và giảm chiều lâu năm 2,5cm thì hai số đo bắt đầu sẽ bằng nhau (hình vuông là hình chữ nhật có chiều dài bằng chiều rộng) suy ra chiều dài thêm hơn chiều rộng là:

2,5 + 2,5 = 5cm.

Bài toán trực thuộc dạng tìm nhì số khi biết tổng cùng hiệu của chúng.

Lời giải:

Nửa chu vi hình chữ nhật là: 54 : 2 = 27 (cm)

Tăng chiều rộng 2,5cm và sút chiều nhiều năm 2,5cm thì được hình vuông. Vậy chiều dài ra hơn nữa chiều rộng lớn là:

2,5 + 2,5 = 5 (cm)

Chiều nhiều năm hình chữ nhật là:

(27 + 5) : 2 = 16 (cm)

Chiều rộng lớn hình chữ nhật là:

27 – 16 = 11 (cm)

Diện tích hình chữ nhật thuở đầu là:

16 x 11 = 176 (cm2).

Đáp số: 176cm2.

Ví dụ 5. Người ta không ngừng mở rộng mảnh vườn hình vuông về tứ phía từng phía 4m. Sau khi mở rộng, diện tích s mảnh vườn tăng lên 192m2. Tìm diện tích mảnh sân vườn cũ.

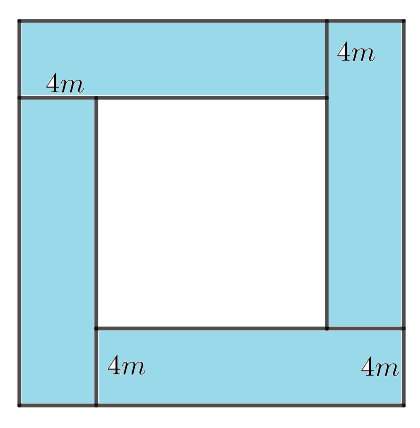
Phân tích tìm phía giải.

Ta có hình vẽ minh họa như sau

Chia phần diện tích tăng thêm 4 hình chữ nhật có chiều rộng lớn 4m, chiều dài là cạnh hình vuông thuở đầu cộng 4m. Tứ hình chữ nhật này có diện tích bằng nhau mà đề bài bác lại cho thấy diện tích miếng vườn tăng lên 192m2 => tính được diện tích mỗi hình => tính được chiều lâu năm hình chữ nhật => tính được cạnh hình vuông => tính được diện tích mảnh sân vườn cũ.

Lời giải:

Vì diện tích tăng thêm 192m2 nên diện tích mỗi hình chữ nhật là:

192 : 4 = 48 (m)

Chiều nhiều năm của mỗi hình chữ nhật này là:

48 : 4 = 12 (m)

Cạnh của hình vuông vắn là:

12 – 4 = 8 (m)

Diện tích của miếng vườn ban sơ là:

8 x 8 = 64 (m2)

Đáp số: 64m2.

Ví dụ 6. Một hình chữ nhật giả dụ tăng chiều rộng để bởi chiều dài của chính nó thì diện tích tăng lên 20cm2, khi giảm chiều dài cho bởi chiều rộng lớn thì diện tích giảm đi 16cm2. Tính diện tích s hình chữ nhật ban đầu?

Phân tích tìm phía giải.

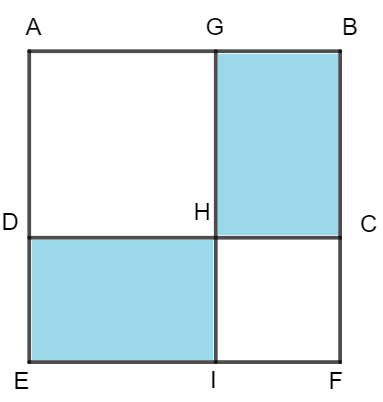
Nhìn vào hình vẽ, ta thấy

Khi tăng chiều rộng bằng chiều dài, diện tích tạo thêm 20cm2 chính là diện tích của hình chữ nhật DCFE.

Khi bớt chiều dài bởi chiều rộng, diện tích giảm đi 16cm2 chính là diện tích của hình chữ nhật GBCH.

Vẽ hình chữ nhật DHIE gồm các form size bằng cùng với hình chữ nhật GBCH.

Hiệu diện tích của hình chữ nhật DCFE với hình chữ nhật DHIE là diện tích hình vuông vắn HCFI có size bằng hiệu chiều dài cùng chiều rộng của hình chữ nhật ban đầu. Hình vuông này công thêm được cạnh tự đó, tìm được các kích cỡ còn lại của hình chữ nhật.

Lời giải:

Có HC = HI (cùng bằng hiệu chiều dài và chiều rộng của hình chữ nhật ban đầu). Hiệu của diện tích tạo thêm và diện tích s giảm đi thiết yếu bằng diện tích s của hình vuôn HCFI, hiệu kia là:

20 – 16 = 4 (cm2)

Do 4 = 2 x 2 cần độ nhiều năm cạnh HC là 2cm.

Cạnh DH giỏi chiều rộng của hình chữ nhật ban đầu là:

16 : 2 = 8 (cm)

Chiều lâu năm của hình chữ nhật ban sơ là:

8 + 2 = 10 (cm)

Diện tích hình chữ nhật thuở đầu là:

8 x 10 = 80 (cm2)

Đáp số: 80cm2

Bài tập dượt tập.

Bài 1. Một miếng vườn cửa hình chữ nhật gồm chiều nhiều năm bằng gấp đôi chiều rộng. Trường hợp tăng chiều rộng lớn thêm 2m và bớt chiều lâu năm 2m thì diện tích s miếng vườn tăng thêm 12m2. Hỏi diện tích s miếng vườn ban sơ là bao nhiêu mét vuông?

Bài 2. Nếu giảm chiều nhiều năm của miếng bìa hình chữ nhật đi 2cm thì ta được một hình vuông vắn thì chu vi 12cm. Tính diện tích s miếng bìa hình chữ nhật.

Bài 3. cho tam giác ABCD có đáy nhỏ xíu là AB, tổng độ dài hai lòng của hình thang là 44cm. Nếu mở rộng đáy lớn thêm 10cm thì diện tích hình thang sẽ tăng thêm 60cm2. Tính diện tích s hình thang ABCD.

Bài 4. đến hình thang vuông ABCD (góc A vuông, đáy bé nhỏ AB) bao gồm AB = 6cm, AD = 10cm. Nếu như thu nhỏ hình thang này thành hình chữ nhật cơ mà vẫn không thay đổi đáy nhỏ bé thì diện tích giảm đi 40cm2. Tính diện tích hình thang ban đầu.

Bài 5. đến hình thang ABCD có đáy nhỏ xíu AB =1dm, nếu bớt đáy to đi 8cm thì diện tích giảm đi 64cm2 đôi khi ta được một hình bình hành. Tìm diện tích s hình thang.

Bài 6. gồm một hình vuông và một hình chữ nhật. Cho thấy thêm cạnh hình vuông vắn bằng chiều dài hình chữ nhật. Chu vi hình vuông lớn hơn chu vi hình chữ nhật là 32m. Diện tích hình vuông vắn lớn hơn diện tích hình chữ nhật là 384m2. Tính diện tích s mỗi hình.

Bài 7. cho một hình chữ nhật, giả dụ ta bớt chiều nhiều năm đi 5cm cùng tăng chiều rộng thêm 5cm thì ta được một hình vuông có diện tích s 144cm2. Tính diện tích hình chữ nhật ban đầu.