CÁC DẠNG BÀI TẬP LƯỢNG GIÁC, PHƯƠNG TRÌNH LƯỢNG GIÁC CHỌN LỌC
Tổng thích hợp các dạng bài xích tập phương trình lượng giác lớp 11 thường chạm mặt để chúng ta tham khảo.
Bạn đang xem: Các dạng bài tập lượng giác
Các dạng bài bác tập phương trình lượng giác lớp 11
♣ Dạng số 1: Giải phương trình lượng giác cơ bản
→ phương thức giải: Dùng những công thức nghiệm khớp ứng với từng pt (phương trình)
Ví dụ minh họa: các bạn hãy giải các phương trình lượng giác sau:
a) sinx = sin(π/6).
c) tanx – 1 = 0
b) 2cosx = 1.
d) cotx = tan2x.
Lời giải bỏ ra tiết
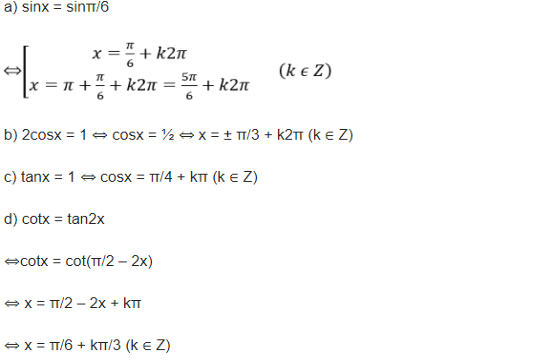
♣ Dạng số 2: Phương trình hàng đầu có một lượng chất giác
→ cách thức giải: Đưa về phương trình cơ bản, lấy ví dụ như asinx + b = 0 ⇔ sinx = -b/a
Ví dụ minh họa:
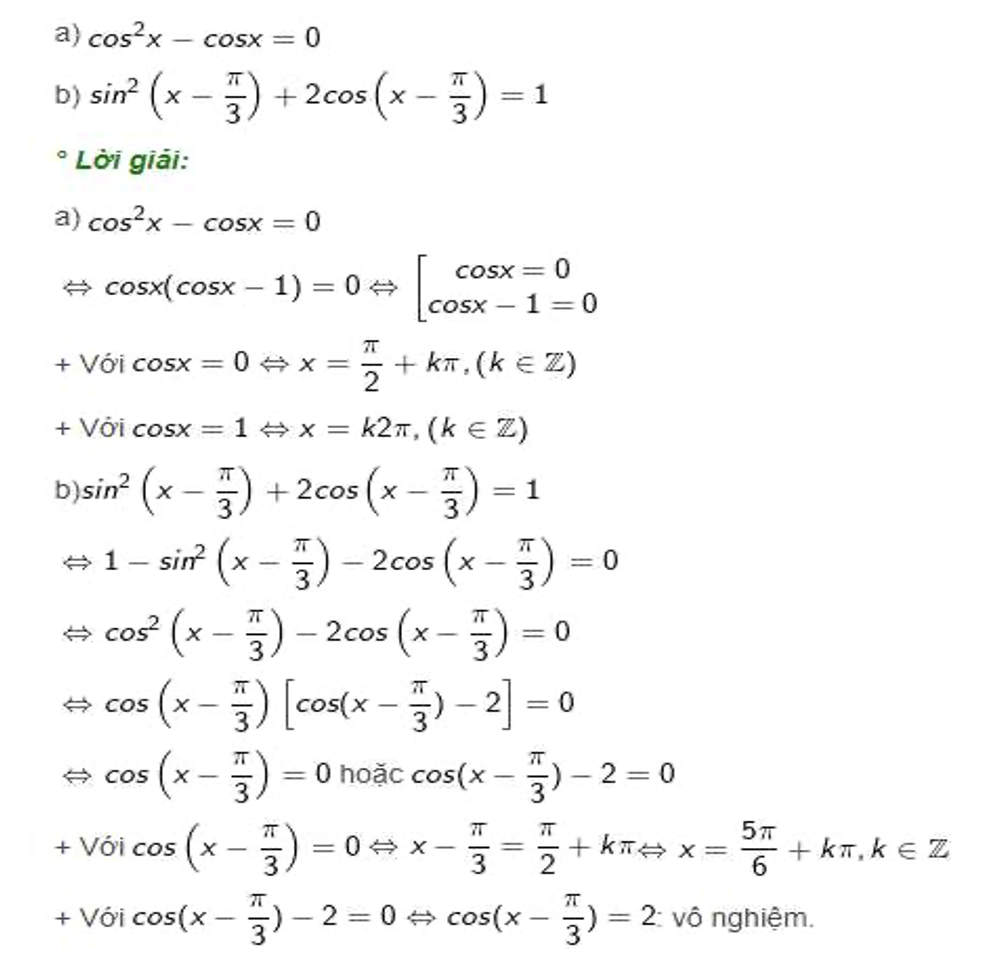
♣ Dạng số 3: Phương trình bậc hai bao gồm một hàm vị giác

♣ Dạng số 4: Phương trình hàng đầu theo sinx với cosx
Xét phương trình tất cả dạng asinx + bcosx = c (1) với a, b chính là các số thực khác 0.


♣ Dạng số 5: Phương trình lượng giác đối xứng, phản đối xứng
Phương trình đối xứng là pt (phương trình) có dạng như sau:
a(sinx + cosx) + bsinxcosx + c = 0 (3)
Phương pháp giải chi tiết:
Để có thể giải phương trình trên bọn họ sử dụng phép đặt ẩn phụ:
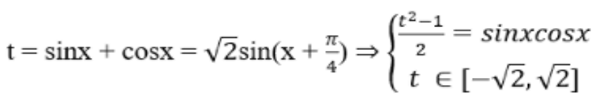
Thay vào (3) ta sẽ được phương trình bậc hai theo t.
* bên cạnh đó chúng ta còn gặp gỡ pt (phương trình) phản đối xứng nó gồm dạng như sau:
a(sinx – cosx) + bsinxcosx + c = 0 (4)

Bài tập phương trình lượng giác thường gặp lớp 11 bao gồm đáp án
♣ bài bác tập phương trình lượng giác cơ bạn dạng có đáp án
Bài 1: Giải những phương trình lượng giác cơ bản saua) cos(3x + π) = 0
b) cos (π/2 – x) = sin2x
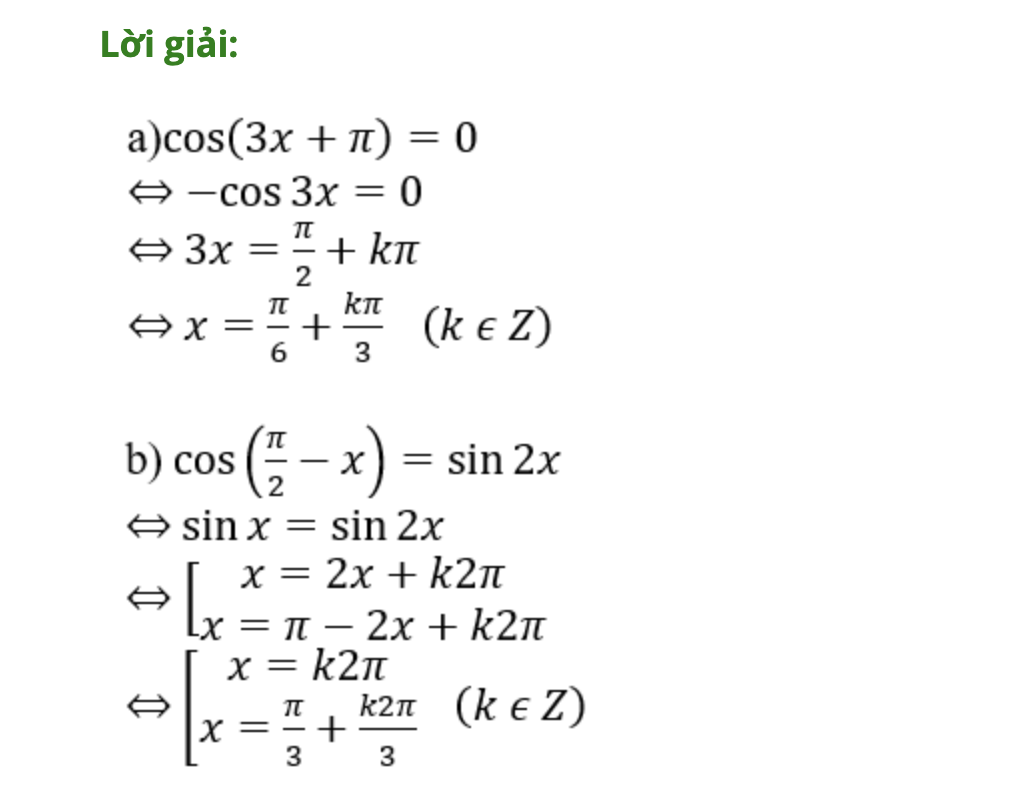
a) sinx.cosx = 1
b) cos2 x – sin2 x + 1 = 0

a) cos2 x – 3cosx + 2 = 0
b) 1/(cos2 x) – 2 = 0

♣ bài tập phương trình bậc hai với một hàm con số giác bao gồm đáp án
Bài tập giải phương trình bậc hai với một hàm con số giác bao gồm đáp ánBài tập giải phương trình bậc nhì với một hàm con số giác kèm đáp ánBài tập dạng phương trình bậc nhì với một hàm con số giác có đáp án♣ bài tập phương trình số 1 theo sinx với cosx có đáp án
Bài tập phương trình hàng đầu theo sinx cùng cosx tất cả đáp ánBài tập giải phương trình số 1 theo sinx với cosx gồm đáp ánBài tập giải phương trình bậc nhất theo sinx với cosx kèm đáp ánBài tập dạng giải phương trình bậc nhất theo sinx cùng cosx kèm đáp án♣ bài bác tập phương trình đẳng cấp và sang trọng bậc 2, bậc 3 lượng giác có đáp án
Bài tập phương trình đẳng cấp và sang trọng bậc 2, bậc 3 lượng giác bao gồm đáp ánBài tập giải phương trình sang trọng bậc 2, bậc 3 lượng giác bao gồm đáp ánBài tập dạng phương trình đẳng cấp và sang trọng bậc 2, bậc 3 lượng giác gồm đáp án♣ bài bác tập phương trình lượng giác đối xứng, làm phản đối xứng có đáp án
Bài tập phương trình lượng giác đối xứng, phản nghịch đối xứng có đáp ánBài tập giải phương trình lượng giác đối xứng, phản đối xứng bao gồm đáp ánBài tập dạng phương trình lượng giác đối xứng, phản bội đối xứng tất cả đáp ánBài tập dạng phương trình lượng giác đối xứng, phản đối xứng kèm đáp án♣ bài xích tập phương trình lượng giác quan trọng đặc biệt có đáp án
Bài tập phương trình lượng giác đặc trưng có đáp ánBài tập giải phương trình lượng giác quan trọng có đáp ánBài tập dạng phương trình lượng giác quan trọng có đáp ánBài tập phương trình lượng giác quan trọng đặc biệt kèm đáp án♣ bài tập kiếm tìm nghiệm của phương trình lượng giác vừa lòng điều kiện có đáp án
Bài tập kiếm tìm nghiệm của phương trình lượng giác thỏa mãn nhu cầu điều kiện gồm đáp ánBài tập dạng tìm nghiệm của phương trình lượng giác thỏa mãn nhu cầu điều kiện có đáp ánBài tập dạng tìm kiếm nghiệm của phương trình lượng giác vừa lòng điều kiện kèm đáp ánBài tập dạng tìm nghiệm của phương trình lượng giác thỏa mãn nhu cầu điều kiện bao gồm đáp án bỏ ra tiếtBộ bài bác tập hàm con số giác 11 để các bạn ôn luyện
Dưới đấy là tổng hợp bài tập hàm số lượng giác 11 cùng với hàm số lượng giác 11 lý thuyết đi kèm để các bạn có thể dễ dàng vận dụng giải bài xích tập.




































Các dạng toán phương trình lượng giác, phương pháp giải và bài bác tập từ cơ bạn dạng đến nâng cao - toán lớp 11
Sau khi có tác dụng quen với những hàm lượng giác thì những dạng bài bác tập về phương trình lượng giác đó là nội dung tiếp theo mà những em sẽ học trong chương trình toán lớp 11.
Vậy phương trình lượng giác có các dạng toán nào, phương pháp giải ra sao? họ cùng tò mò qua nội dung bài viết này, đồng thời áp dụng các phương pháp giải này để gia công các bài bác tập từ cơ phiên bản đến cải thiện về phương trình lượng giác.
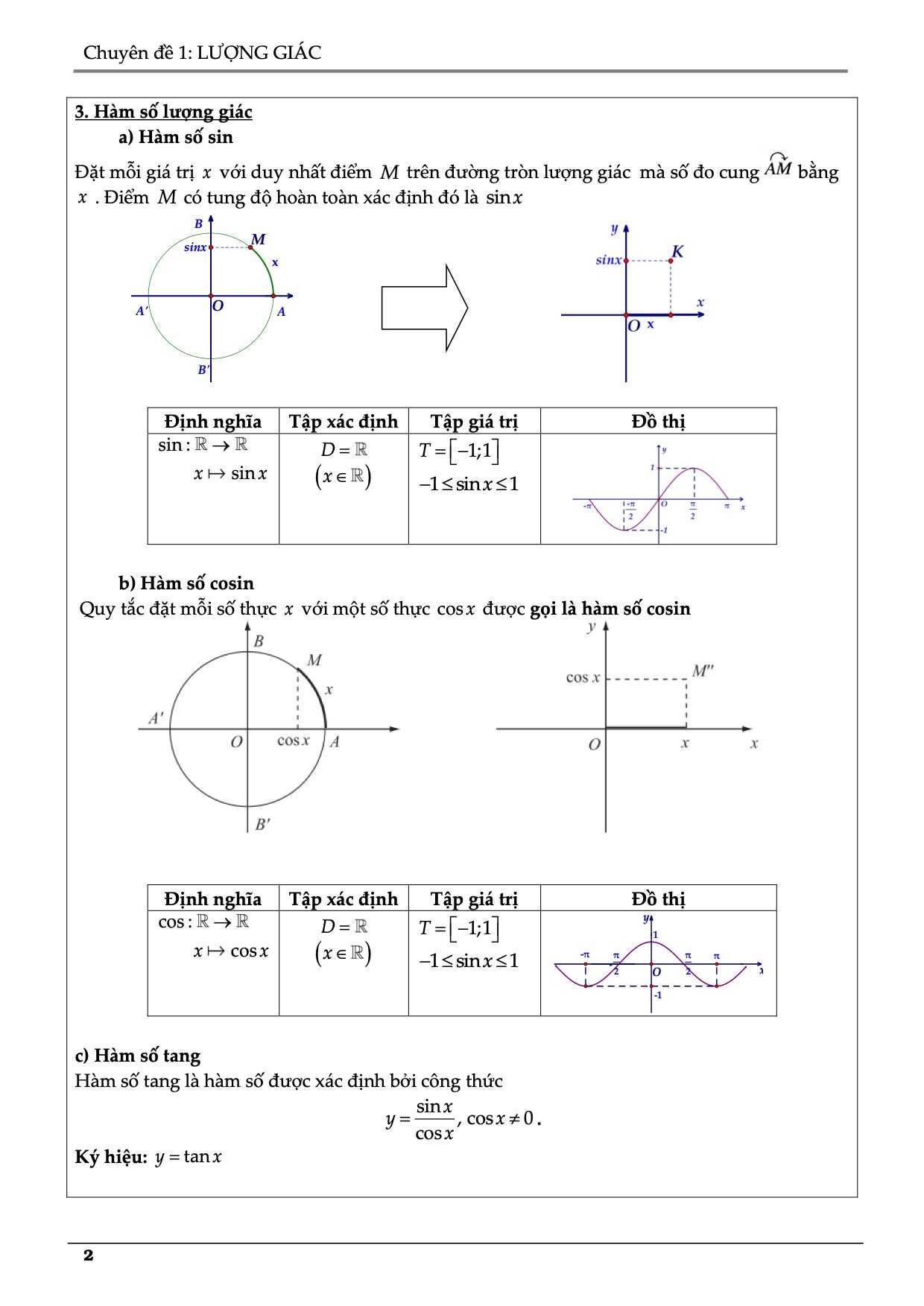
I. Triết lý về Phương trình lượng giác
1. Phương trình sinx = a. (1)
° |a| > 1: Phương trình (1) vô nghiệm
° |a| ≤ 1: gọi α là một cung thỏa sinα = a, lúc ấy phương trình (1) có các nghiệm là:
x = α + k2π, ()
và x = π - α + k2π, ()
- Nếu α thỏa mãn nhu cầu điều kiện
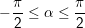
x = arcsina + k2π, ()
và x = π - arcsina + k2π, ()
- Phương trình sinx = sinβ0 có những nghiệm là:
x = β0 + k3600, ()
và x = 1800 - β0 + k3600, ()
2. Phương trình cosx = a. (2)
° |a| > 1: Phương trình (2) vô nghiệm
° |a| ≤ 1: gọi α là một cung thỏa cosα = a, khi đó phương trình (2) có các nghiệm là:
x = ±α + k2π, ()
- Nếu α vừa lòng điều kiện 0 ≤ α ≤ π cùng cosα = a thì ta viết α = arccosa. Lúc đó các nghiệm của phương trình (2) là:
x = ±arccosa + k2π, ()
- Phương trình cosx = cosβ0 có các nghiệm là:
x = ±β0 + k3600, ()
3. Phương trình tanx = a. (3)
- Tập xác định, hay điều kiện của phương trình (3) là:
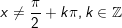
- Nếu α vừa lòng điều kiện
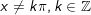
- Nếu α thỏa mãn nhu cầu điều khiếu nại

II. Những dạng toán về Phương trình lượng giác và cách thức giải
° Dạng 1: Giải phương trình lượng giác cơ bản
* Phương pháp
- Dùng các công thức nghiệm tương ứng với từng phương trình.
* lấy ví dụ 1 (Bài 1 trang 28 SGK Đại số và Giải tích 11): Giải những phương trình sau:
a) b)
b)
d)
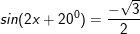
* giải thuật bài 1 trang 28 SGK Đại số và Giải tích 11:
a)
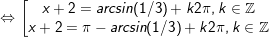
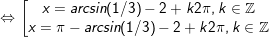
b)
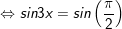
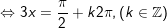
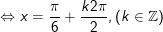
c)
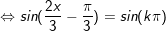
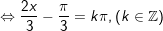
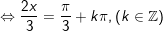
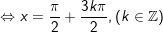
d)
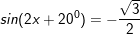
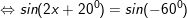
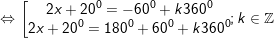
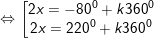
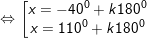
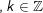
* lấy ví dụ 2: Giải các phương trình sau:
a)
b)
c)
d)
° Lời giải:
a)
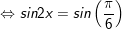
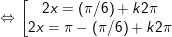
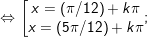
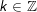
b)
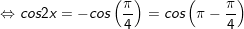
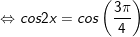
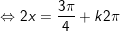
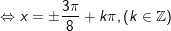
c)
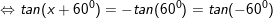
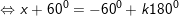
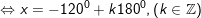
d)
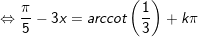
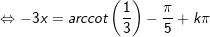
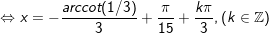
° Dạng 2: Giải một trong những phương trình lượng giác đưa được về dạng PT lượng giác cơ bản
* Phương pháp
- Dùng các công thức biến đổi để đưa về phương trình lượng giác đã cho về phương trình cơ bạn dạng như Dạng 1.
* ví dụ 1: Giải các phương trình sau:
a)
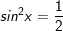
b)
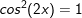
c)
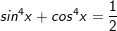
d)
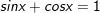
° Lời giải:
a)
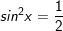
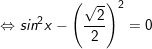
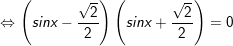
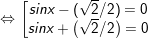
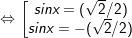
+ Với
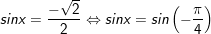
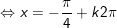
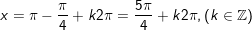
+ cùng với
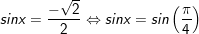
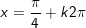
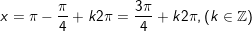
b)
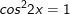
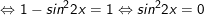
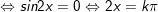
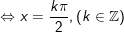
c)
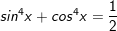
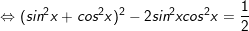
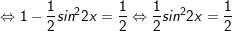
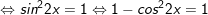
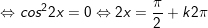
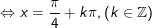
d)
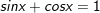
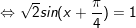
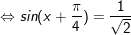
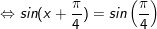
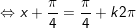
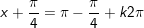
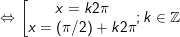
* lưu ý: Bài toán trên áp dụng công thức:
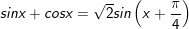
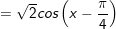
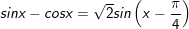
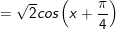
* lấy ví dụ như 2: Giải các phương trình sau:
a)
b)
° Lời giải:
a)
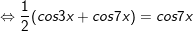
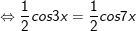
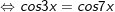
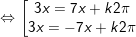
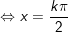
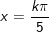
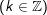
b)
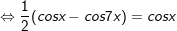
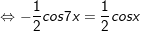
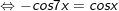
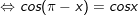
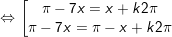
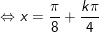
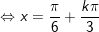
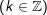
* lưu giữ ý: bài toán vận dụng công thức chuyển đổi tích thành tổng:
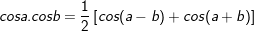
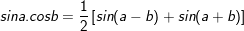
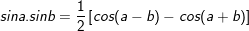
* lấy ví dụ 3: Giải những phương trình sau:
a)1 + 2cosx + cos2x = 0
b)cosx + cos2x + cos3x = 0
c)sinx + sin2x + sin3x + sin4x = 0
d)sin2x + sin22x = sin23x
° Lời giải:
a)
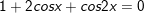
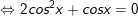
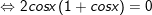
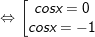
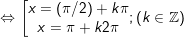
b)
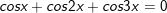
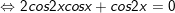
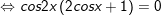
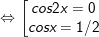
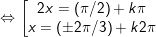
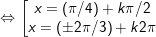
c)
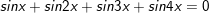
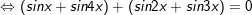
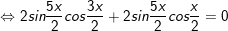
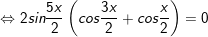
hoặc
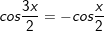
hoặc
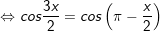
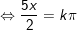
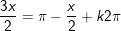
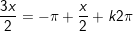
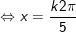
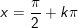
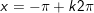
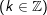
d)
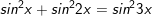
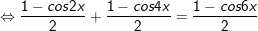
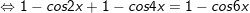
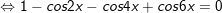
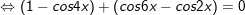
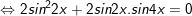
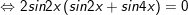
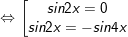
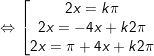
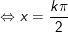
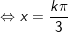
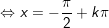
* lưu lại ý: Bài toán bên trên có áp dụng công thức biến hóa tổng các kết quả và công thức nhân đôi:
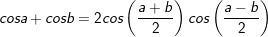
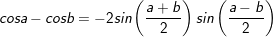
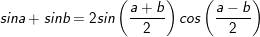
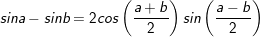
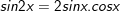
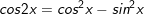
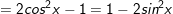
° Dạng 3: Phương trình số 1 có một hàm số lượng giác
* Phương pháp
- Đưa về dạng phương trình cơ bản, ví dụ:
* ví dụ như 1: Giải các phương trình sau:
a)
b)
° Lời giải:
a)
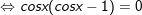
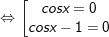
+ Với
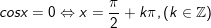
+ Với
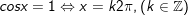
b)
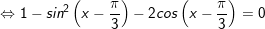
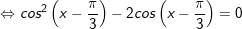
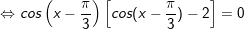
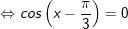
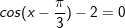
+ Với
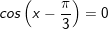
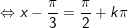
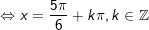
+ Với
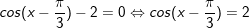
Xem thêm: Giải vở bài tập địa lý 9 hay, ngắn nhất, giải vở bài tập địa lí lớp 9 hay, ngắn nhất
° Dạng 4: Phương trình bậc hai bao gồm một hàm con số giác
* Phương pháp
♦ Đặt ẩn phụ t, rồi giải phương trình bậc hai so với t, ví dụ:
+ Giải phương trình: asin2x + bsinx + c = 0;
+ Đặt t=sinx (-1≤t≤1), ta tất cả phương trình at2 + bt + c = 0.
* lưu giữ ý: Khi để t=sinx (hoặc t=cosx) thì phải tất cả điều kiện: -1≤t≤1
* lấy ví dụ như 1: Giải những phương trình sau
a)
b)
° Lời giải:
a)
- Đặt
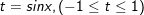
⇔ t = 1 hoặc t = 1/2.
+ cùng với t = 1: sinx = 1
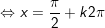
+ với t=1/2:
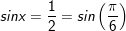
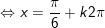
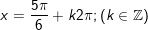
b)
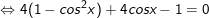
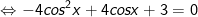
+ Đặt
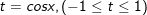
⇔ t = 3/2 hoặc t = -1/2.
+ t = 3/2 >1 bắt buộc loại
+
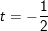
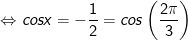
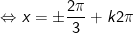
* Chú ý: Đối với phương trình dạng: asin2x + bsinx.cosx + c.cos2x = 0, (a,b,c≠0). Cách thức giải như sau:
- Ta có: cosx = 0 không hẳn là nghiệm của phương trình do a≠0,
Chia 2 vế đến cos2x, ta có:atan2x + btanx + c = 0 (được PT bậc 2 với tanx)
- ví như phương trình dạng: asin2x + bsinx.cosx + c.cos2x = d thì ta nuốm d = d.sin2x + d.cos2x, cùng rút gọn đem lại dạng trên.
° Dạng 5: Phương trình dạng: asinx + bcosx = c (a,b≠0).
* Phương pháp
◊ cách 1: Chia nhì vế phương trình cho , ta được:
- Nếu thì phương trình vô nghiệm
- Nếu thì đặt
(hoặc )
- Đưa PT về dạng: (hoặc ).
◊ bí quyết 2: Sử dụng bí quyết sinx cùng cosx theo ;
- Đưa PT về dạng phương trình bậc 2 đối với t.
* lưu lại ý: PT: asinx + bcosx = c, (a≠0,b≠0) bao gồm nghiệm lúc c2 ≤ a2 + b2
• Dạng tổng quát của PT là:asin
* Ví dụ: Giải những phương trình sau:
a)
b)
° Lời giải:
a)
+ Ta có:
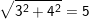
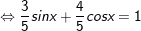
+ Đặt
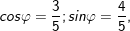
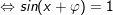
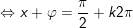
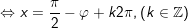
b)
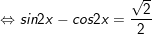
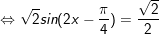
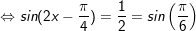
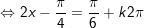
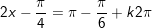
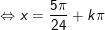
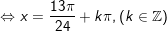
* lưu lại ý: bài bác toán áp dụng công thức:
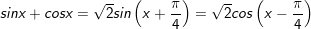
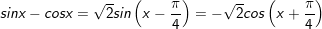
° Dạng 6: Phương trình đối xứng cùng với sinx và cosx
a(sinx + cosx) + bsinx.cosx + c = 0 (a,b≠0).
* Phương pháp
- Đặt t = sinx + cosx, khi đó: thay vào phương trình ta được:
bt2 + 2at + 2c - b = 0 (*)
- lưu ý: 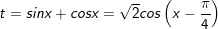
- vì thế sau khi tìm được nghiệm của PT (*) đề nghị kiểm tra (đối chiếu) lại đk của t.
- Phương trình dạng: a(sinx - cosx) + bsinx.cosx + c = 0 không hẳn là PT dạng đối xứng nhưng cũng hoàn toàn có thể giải bằng phương pháp tương tự:
Đặt t = sinx - cosx; 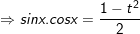
* Ví dụ: Giải các phương trình sau:
a) 2(sinx + cosx) - 4sinx.cosx - 1 = 0
b) sin2x - 12(sinx + cosx) + 12 = 0
° Lời giải:
a) 2(sinx + cosx) - 4sinx.cosx - 1 = 0
+ Đặt t = sinx + cosx, , khi đó: thay vào phương trình ta được:
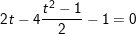
hoặc
+ Với 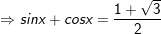
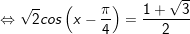
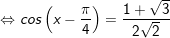
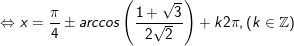
+ Tương tự, với 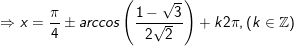
b) sin2x - 12(sinx + cosx) + 12 = 0
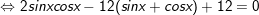
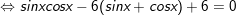
- Đặt t = sinx + cosx, , khi đó: thay vào phương trình ta được:
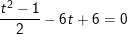
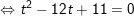
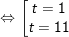
+ với t=1 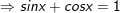
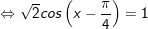
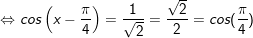
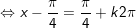
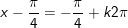
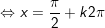
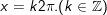
+ Với 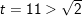
III. Bài bác tập về những dạng toán Phương trình lượng giác
* Bài 2 (trang 28 SGK Đại số và Giải tích 11): Với đa số giá trị như thế nào của x thì giá trị của các hàm số y = sin 3x cùng y = sin x bằng nhau?
° giải mã bài 2 trang 28 SGK Đại số cùng Giải tích 11:
- Ta có:
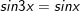
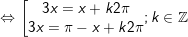
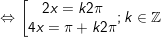
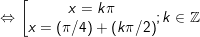
- Vậy với
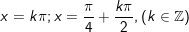
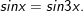
* bài xích 3 (trang 28 SGK Đại số 11): Giải các phương trình sau:
a)
b)
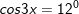
c)
d)
° giải mã bài 3 trang 28 SGK Đại số cùng Giải tích 11:
a)
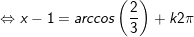
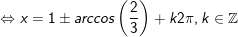
- Kết luận: PT bao gồm nghiệm
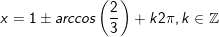
b) cos3x = cos12º
⇔ 3x = ±12º + k.360º , k ∈ Z
⇔ x = ±4º + k.120º , k ∈ Z
- Kết luận: PT gồm nghiệm x = ±4º + k.120º , k ∈ Z
c)
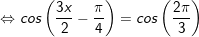
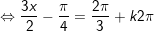
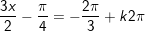
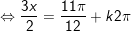
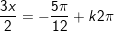
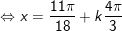
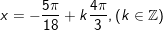
d)
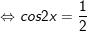
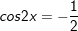
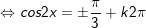
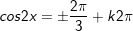
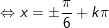
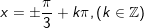
* Bài 4 (trang 29 SGK Đại số cùng Giải tích 11): Giải phương trình
° giải mã bài 3 trang 28 SGK Đại số với Giải tích 11:
- Điều kiện: sin2x≠1
- Ta có:
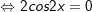
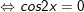
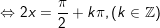
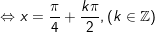
+ Đến đây ta cần so sánh với điều kiện:
- Xét k lẻ tức là: k = 2n + 1
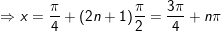
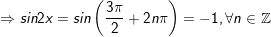
- Xét k chẵn tức là: k = 2n
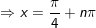
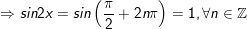
- Kết luận: Vậy PT gồm họ nghiệm là
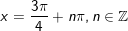
* Bài 1 (trang 36 SGK Đại số cùng Giải tích 11): Giải phương trình: sin2x – sinx = 0
° giải mã bài 1 trang 36 SGK Đại số và Giải tích 11:
- Ta có: sin2x – sinx = 0
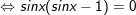
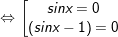
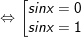
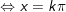
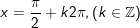
- Kết luận: PT tất cả tập nghiệm
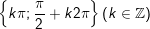
* bài 2 (trang 36 SGK Đại số với Giải tích 11): Giải những phương trình sau:
a) 2cos2x – 3cosx + 1 = 0
b) 2sin2x +
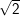
° lời giải bài 2 trang 36 SGK Đại số cùng Giải tích 11:
a) 2cos2x – 3cosx + 1 = 0 (1)
- Đặt t = cosx, điều kiện: –1 ≤ t ≤ 1, khi ấy PT (1) trở thành: 2t2 – 3t + 1 = 0
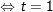
+ với t = 1 ⇒ cosx = 1 ⇔ x = k2π, (k ∈ Z)
+ Với
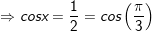
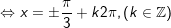
- Kết luận: PT tất cả nghiệm là
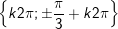
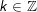
Hy vọng với nội dung bài viết hệ thống về các dạng toán phương trình lượng giác và phương thức giải cùng những bài tập áp dụng từ cơ phiên bản đến nâng cao sinh sống trên giúp ích cho các em. Mọi góp ý với thắc mắc các em vui lòng để lại phản hồi dưới bài viết để Hay học hỏi và chia sẻ ghi nhận cùng hỗ trợ, chúc những em học tốt.









